Semantic Image Inpainting for Medical Images with Deep Generative Models

I took the course Medical Image Computing in Spring 2019 offered by Prof. Suyash Awate at IIT Bombay. This is a blog post about the work I did for the course project with Pranav Kulkarni on using GANs for image inpainting based on work by R. Yeh et al. in CVPR 2017 and extending it to use VAE for the same problem and showing that VAEs perform better than GANs for our task.

The motivation behind image inpainting for medical images comes from the need for pre-processing images with lesions for downstream tasks like segmentation or registration. The idea behind using a deep generative model is to use strong priors and use the given context to understand high-level features to fill the missing regions in the images. An example of a natural image is shown below where the inpainting algorithm must derive the information about characteristics from the partial face and use prior knowledge to construct the missing part of the face.

The goal is to generate the missing content by conditioning on the available data by using generative models (like GANs) where the generator acts as a mapping from latent space to images. Our method is a re-implementation and extension of work by R. Yeh et al. in CVPR 2017. Once our generative model is trained and produces realistic images from random vectors in the latent space, the pipeline for inpainting is followed which has the following main three main steps:

1. For inpainting, we find the closest encoding of the corrupted image in latent space using context loss and prior loss. This is explained in detail below.
2. Pass the encoding through the generative model to infer missing content.
3. Blend the predicted patch intensities to have coherence with surrounding known pixel intensities using blending.

The inference in this method is possible independent of the structure of the missing part. We don’t need to account for the and size of corrupted patches while training the model. This work has provided realistic state of the art results for image inpainting on face images.

The first step needs more clarification here. The latent encoding of the corrupted image is found by using backpropagation to the input. Recall that the input to a generator is a random Gaussian vector with zero mean and unit variance. Using context loss ensures that the encoding of the input actually produces the known content in the output when passed through the generative model. Prior loss is used to ensure that the output image is indeed realistic.

Let $G$ be the generator and $D$ be the discriminator. The context loss is calculated by minimizing the masked $L_1$ norm between the given image $y$ and output image $G(z)$ where $z$ in the estimated latent encoding i.e. for a given mask $M$, context loss is $L_c(z|y,M) = ||W \odot (G(z)-y)||_1$. In the paper, they’ve suggested that giving more weight to pixels on the boundary of the missing region improves the output and we confirmed it in our experiments as well.

Since there are missing portions in the image from which we are deriving the latent vector representation, we need to use the prior loss to ensure realistic outputs. In GANs, this is done by using the discriminator. The prior loss would therefore be $L_p(z) = \lambda \log (1- D(G(z)))$ where $\lambda$ is the prior weight.

Though this process may give a reasonable and well-aligned inpainted image, the predicted pixels may not exactly preserve the same intensities of the surrounding pixels. To correct this, authors have used Poisson blending in the third step. Poisson blending has the following objective function:

The problem turns out to be equivalent to minimizing the norm of the difference of Laplacian of $x$ and $G(z)$ and has a unique solution. We’ve confirmed in our experiments that this step is indeed very crucial for the high quality of final output images.

We wish to extend their work for VAEs, but VAEs where we don’t have a discriminator. We need another prior loss, the most intuitive way is to penalize the norm of $z$ vector itself since its prior is a zero-mean unit variance Gaussian distribution. Therefore, our prior loss is $L_p = \lambda || z ||_2^2$.

The slides from our project presentation can be found here.

Results

We compare VAEs and GANs in two settings, with convolutional kernels size of 3 and 7 on structure MRI slices. The results shown below show that the model indeed performs well giving high PSNR (peak signal-to-noise ratio).

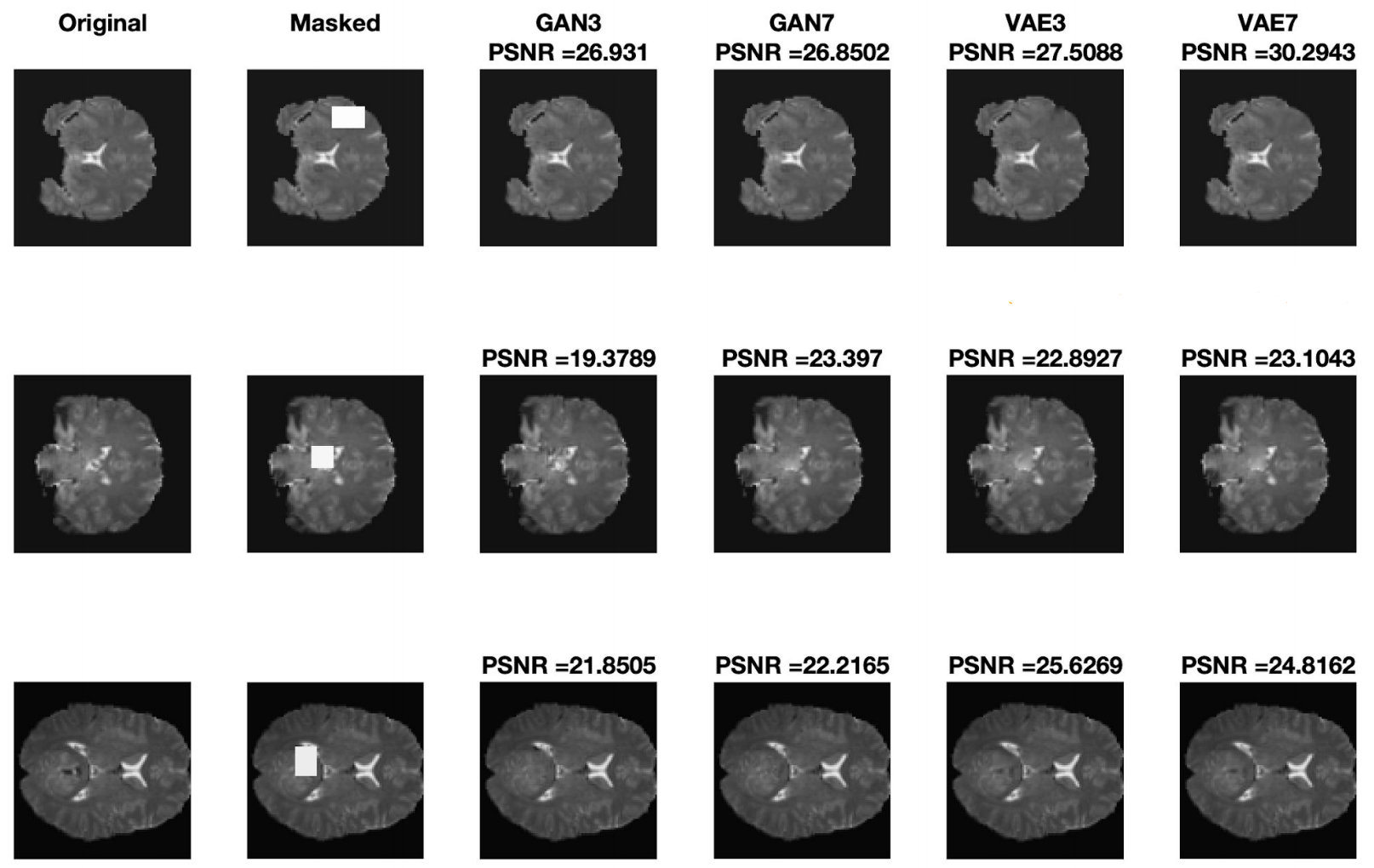
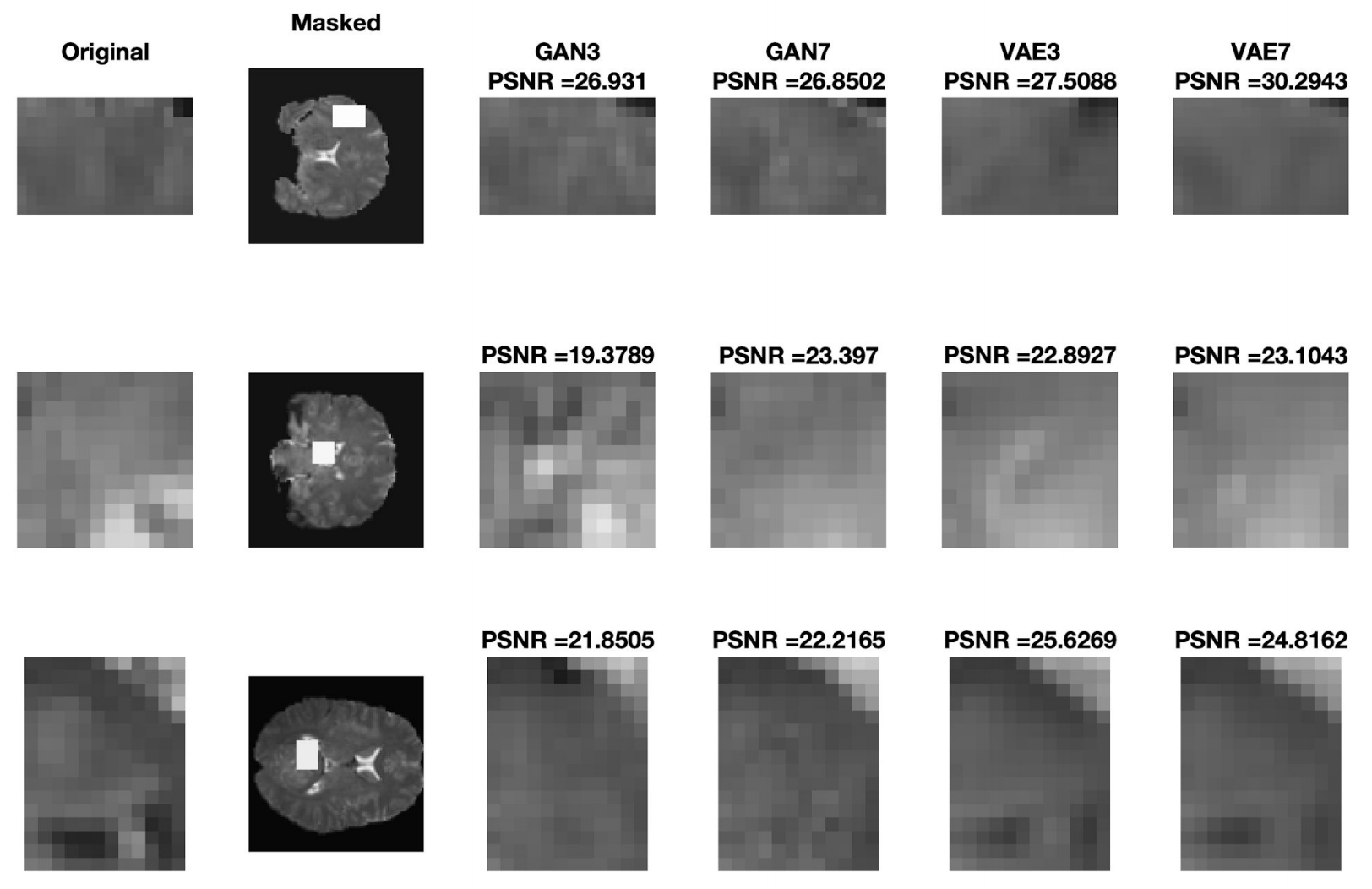
Inpainted images are visually almost indifferentiable. So we zoom into the missing region the image below and observe how VAEs are performing better and larger convolutional kernels help.

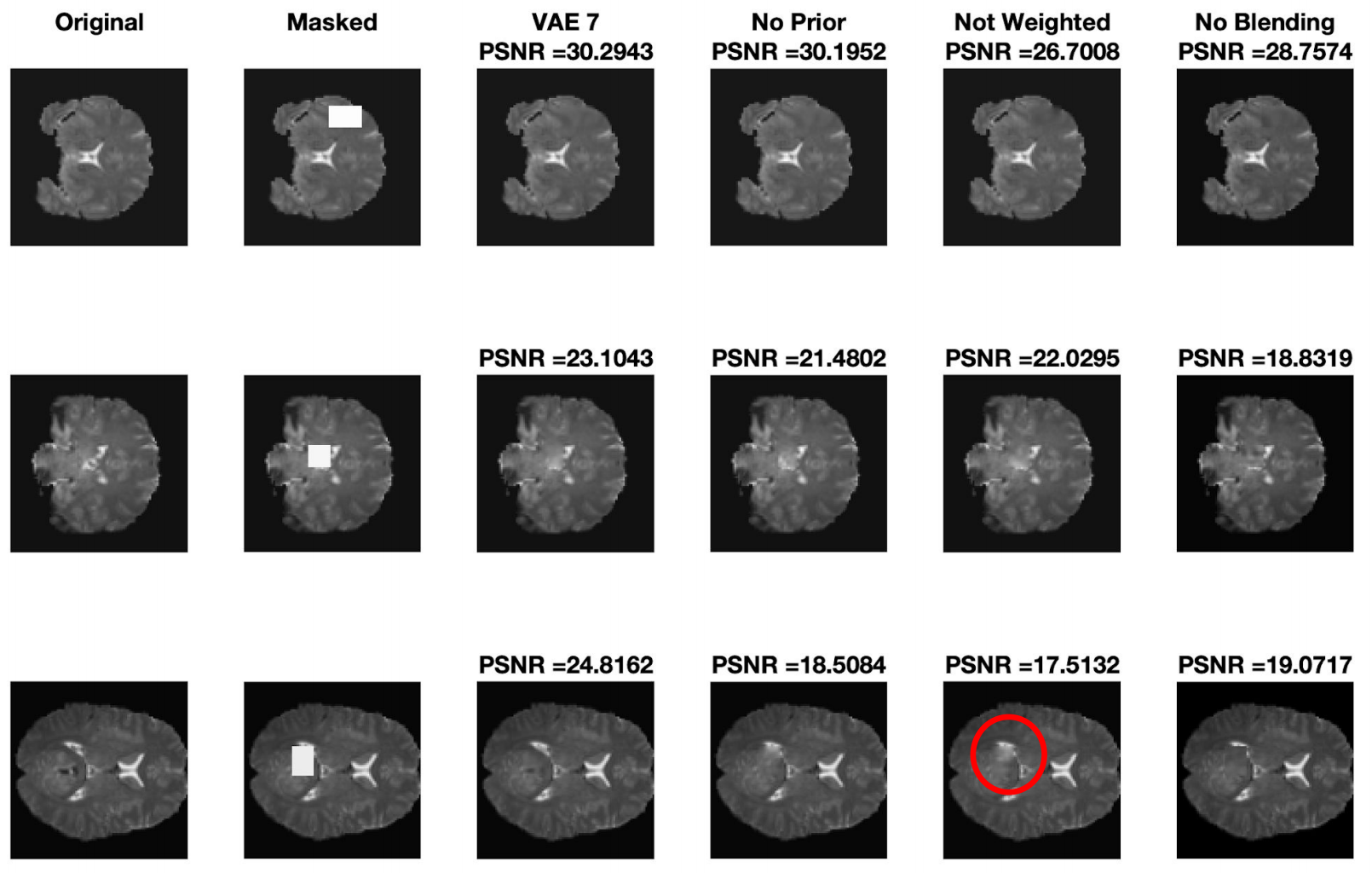
We have done many more experiments that are present in the slides below. In summary, we have shown that VAEs are consistently better in terms of PSNR and SSIM (structural similarity), even for larger patches though more details are missing in every method that we tried. Further, in the image shown below, we see the importance of the prior loss, weighting of context loss and blending by doing an ablation study. The red circle shows a particular example of how weighted context loss plays an important role in image inpainting performance.

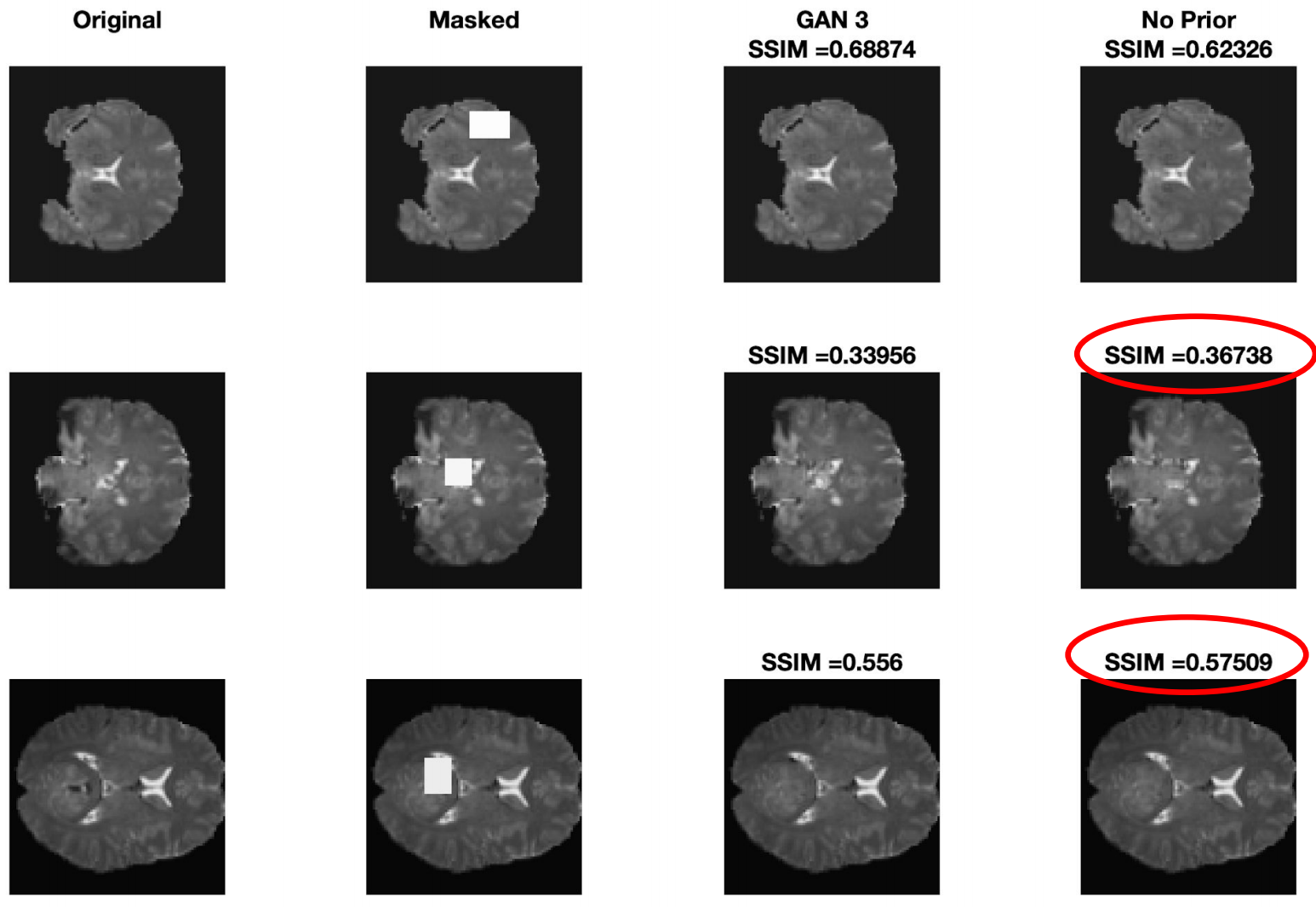
An important observation that we made is that the effect of prior loss in GANs using discriminator is not very prominent, and there are many examples where not using prior gave a better result. A snapshot of this observation is shown below.

Comments and Conclusions

The main question that we need to answer is: why are VAEs performing better than GANs? One plausible reason is that VAEs are explicitly trained to produce real images while the generator in GANs is learned indirectly from the gradients flowing from the discriminator. This can lead to stronger prior influence in VAEs than GANs. Further, in our particular problem, the modes of variations are much lesser than natural images. Because of explicit training, the VAEs can learn the primary modes of variations early in the training. Further, an important advantage of VAEs in our setting is that they were trained in 25% fewer epochs, each consuming 25% less time. Overall VAEs were 78% faster to train.

In our project, we extended the ideas from the aforementioned paper to use VAE for image inpainting on medical images. We showed that VAEs consistently performed better than GANs in terms of PSNR and SSIM metrics and also observed the same visually. We confirmed the importance of the prior loss, weighted context loss, and blending and observed that the advantage due to prior loss is more clearly observed in VAEs than GANs.